Алгебра и все формулы по алгебре

Алгебра — это раздел математики, который занимается математическими символами и правилами обращения с этими символами. Это связующая нить почти всех областей математики, и она используется везде, от решения основных уравнений до изучения абстрактных понятий, таких как группы и поля. По своей сути алгебра — это изучение математических уравнений и их решений.

В алгебре производят манипулирование уравнениями, решают уравнений, изучают свойства уравнений и их решений. Алгебраические уравнения могут включать любое количество переменных, и цель состоит в том, чтобы найти значения этих переменных, которые делают уравнение верным. В основе алгебры лежит использование букв, называемых переменными, для обозначения неизвестных чисел. В основном алгебраические выражения являются буквенными (и использованием переменных) или численными. Например, в уравнении 2x + 3 = 7 буква x представляет собой неизвестное число. Уравнение можно решить относительно x, изолировав его в одной части уравнения и найдя его значение, которое в данном случае равно x = 2. Этот процесс называется решением для переменной.

В алгебре изучаются математические операции, такие как сложение, вычитание, умножение и деление, возведение в степень и то, как эти операции можно применять к уравнениям и переменным. Эти операции можно использовать для упрощения и изменения уравнений, а также для их решения.

Используются такие понятия, как многочлены, которые представляют собой математические выражения, включающие переменные и степени переменных. Например, полином x^2 + 2x + 3 представляет собой квадратное уравнение, и его можно разложить на множители или упростить с помощью различных методов. Помимо уравнений и многочленов, алгебра изучается функции и графики функций (уравнения), а также математические структуры, таких как группы, кольца и поля. Эти структуры используются для изучения абстрактных понятий, таких как симметрия и алгебраические уравнения, в высшей математике, такой как абстрактная алгебра, теория Галуа и теория чисел.

СПРАВОЧНЫЙ МАТЕРИАЛ ПО АЛГЕБРЕ ДЛЯ 7-11 КЛАССОВ.

Содержание

Степень с натуральным показателем.

Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.
Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени.
а⁰=1 Любое число (кроме нуля) в нулевой степени равно единице.
а¹=а Любое число в первой степени равно самому себе.
a^m∙aⁿ=a^m⁺ⁿ При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
a^m:aⁿ=a^m^—ⁿ При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(a^m)ⁿ=a^mn При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)ⁿ=aⁿ∙bⁿ При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)ⁿ=aⁿ/bⁿПри возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Степень с целым показателем.

(- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а, т.е. a^—ⁿ=1/aⁿ. (10^-2=1/10²=1/100=0,01).
(a/b)^—ⁿ=(b/a)ⁿ
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.

Стандартный вид числа.

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10ⁿ, где 1≤а < 10 и n (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

Одночлен.

Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.
Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.
Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Многочлен.

Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.
Двучлен – это многочлен, состоящий из двух членов (одночленов).
Трехчлен – это многочлен, состоящий из трех членов (одночленов).
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.

Действия с одночленами и многочленами.

Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.
Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.

Формулы сокращенного умножения (ФСУ).

(a+b)²=a²+2ab+b²Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)²=a²-2ab+b²Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
a²-b²=(a-b)(a+b) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
(a+b)³=a³+3a²b+3ab²+b³Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a-b)³= a³-3a²b+3ab²-b³Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
a³+b³=(a+b)(a²-ab+b²) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a³-b³=(a-b)(a²+ab+b²) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
(a+b+c)²=a²+b²+c²+2ab+2ac+2bc Квадрат суммы трех выражений равен сумме квадратов этих выражений плюс всевозможные удвоенные попарные произведения самих выражений.
Справка. Полный квадрат суммы двух выражений: a² + 2ab + b²

Неполный квадрат суммы двух выражений: a² + ab + b²

Квадратная функция.

Функцию вида y=x² называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x² направлены вверх.

Кубическая функция.

Функцию вида y=x³ называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x³ находятся в I и III четвертях.

Четная функция

Функция f называется четной, если вместе с каждым значением переменной х из области определения функции значение (-х) также входит в область определения этой функции и при этом выполняется равенство: f(- x)=f(x). График четной функции симметричен относительно оси ординат (Оy). Функция y=x² – четная.

Нечетная функция

Функция f называется нечетной, если вместе с каждым значением переменной х из области определения функции значение (-х) также входит в область определения этой функции и при этом выполняется равенство: f(- x)=- f(x). График нечетной функции симметричен относительно начала координат. Функция y=x³ – нечетная.

Квадратное уравнение

Определение. Уравнение вида ax²+bx+c=0, где a, b и c – любые действительные числа, причем а≠0, х – переменная, называется квадратным уравнением.

a – первый коэффициент, b – второй коэффициент, c – свободный член.

Решение неполных квадратных уравнений

ax²=0 – неполное квадратное уравнение (b=0, c=0). Решение: х=0. Ответ: 0.
ax²+bx=0 – неполное квадратное уравнение (с=0). Решение: x (ax+b)=0 → x₁=0 или ax+b=0 → x₂=-b/a. Ответ: 0; -b/a.
ax²+c=0 – неполное квадратное уравнение (b=0); Решение: ax²=-c → x²=-c/a.

Если (-c/a) < 0, то действительных корней нет. Если (-с/а) > 0, то имеем два действительных корня:

Решение полных квадратных уравнений

ax²+bx+c=0 – квадратное уравнение общего вида

Дискриминант D=b²— 4ac.

Если D > 0, то имеем два действительных корня:

Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).

Если D < 0, то действительных корней нет.

ax²+bx+c=0 – квадратное уравнение частного вида при четном втором

коэффициенте b

ax²+bx+c=0 – квадратное уравнение частного вида при условии: a-b+c=0.

Первый корень всегда равен минус единице, а второй корень равен минус с, деленному на а:

x₁=-1, x₂=-c/a.

ax²+bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0.

Первый корень всегда равен единице, а второй корень равен с, деленному на а:

x₁=1, x₂=c/a.

Решение приведенных квадратных уравнений

x²+px+q=0 – приведенное квадратное уравнение (первый коэффициент равен единице).

Приведенные квадратные уравнения можно решать по тем же формулам, что и полные квадратные уравнения, однако, чаще для решения приведенных квадратных уравнений применяют теорему Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения x²+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p; x₁∙x₂=q.

Теорема Виета для полного квадратного уравнения ax²+bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

x₁+x₂=-b/a; x₁∙x₂=c/a.

Разложение квадратного трехчлена на множители

ax²+bx+c=a·(x-x₁)(x-x₂), где x_1,x₂ - корни квадратного уравнения ax²+bx+c=0.

Числовая последовательность

Функция натурального аргумента называется числовой последовательностью, а числа, образующие последовательность — членами последовательности.

Числовую последовательность можно задать следующими способами: словесным, аналитическим, рекуррентным, графическим.

Арифметическая прогрессия

Определение арифметической прогрессии

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом d, называют арифметической прогрессией. Число d называют разностью арифметической прогрессии. В арифметической прогрессии {a_n}, т. е. в арифметической прогрессии с членами: a₁, a₂, a₃, a₄, a₅, …, a_n-1, a_n, … по определению: a₂=a₁+d; a₃=a₂+d; a₄=a₃+d; a₅=a₄+d; …; a_n=a_n-1+d; …

Формула n-го члена арифметической прогрессии

a_n=a₁+(n-1) d.

Свойства арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:

a_n=(a_n-1+a_n+1):2;

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому равноотстоящих от него членов:

a_n=(a_n-k+a_n+k):2.

Формулы суммы первых n членов арифметической прогрессии

1) S_n= (a₁+a_n)∙n/2; 2) S_n=(2a₁+(n-1) d)∙n/2

Геометрическая прогрессия

Определение геометрической прогрессии

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число q, называют геометрической прогрессией прогрессией. Число q называют знаменателем геометрической прогрессии. В геометрической прогрессии {b_n}, т. е. в геометрической прогрессии b₁, b₂, b₃, b₄, b₅, … , b_n, … по определению: b₂=b₁∙q; b₃=b₂∙q; b₄=b₃∙q; … ; b_n=b_n_-1∙q.

Формула n-го члена геометрической прогрессии

b_n=b₁∙qⁿ^-1.

Свойства геометрической прогрессии

Формула суммы первых n членов геометрической прогрессии

Сумма бесконечно убывающей геометрической прогрессии

Перевод бесконечной периодической десятичной дроби в обыкновенную дробь

Бесконечная периодическая десятичная дробь равна обыкновенной дроби, в числителе которой разность между всем числом после запятой и числом после запятой до периода дроби, а знаменатель состоит из «девяток» и «нулей», причем, «девяток» столько, сколько цифр в периоде, а «нулей» столько, сколько цифр после запятой до периода дроби. Пример:

Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника

(α+β=90°)

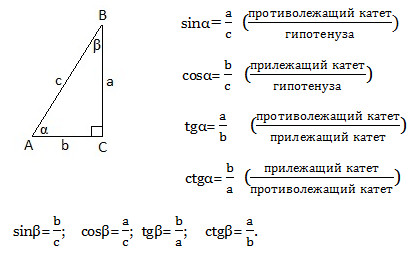
Имеем: sinβ=cosα; cosβ=sinα; tgβ=ctgα; ctgβ=tgα. Так как β=90°-α, то

sin (90°-α)=cosα; cos (90°-α)=sinα;

tg (90°-α)=ctgα; ctg (90°-α)=tgα.

Кофункции углов, дополняющих друг друга до 90°, равны между собой.

Основные тригонометрические тождества

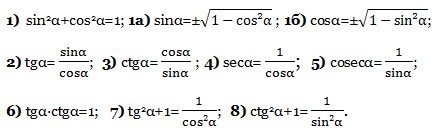
Формулы сложения

9) sin (α+β)=sinα∙cosβ+cosα∙sinβ;

10) sin (α-β)=sinα∙cosβ-cosα∙sinβ;

11) cos (α+β)=cosα∙cosβ-sinα∙sinβ;

12) cos (α-β)=cosα∙cosβ+sinα∙sinβ;

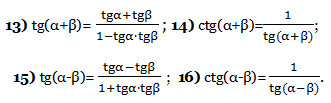
Формулы двойного и тройного аргументов

17) sin2α=2sinαcosα; 18) cos2α=cos²α-sin²α;

19) 1+cos2α=2cos²α; 20) 1-cos2α=2sin²α

21) sin3α=3sinα-4sin³α; 22) cos3α=4cos³α-3cosα;

Формулы преобразования суммы (разности) в произведение

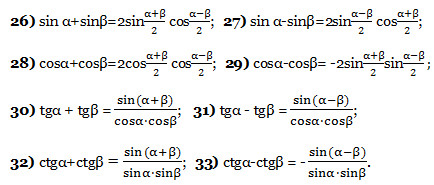
Формулы преобразования произведения в сумму (разность)

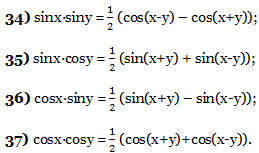
Формулы половинного аргумента

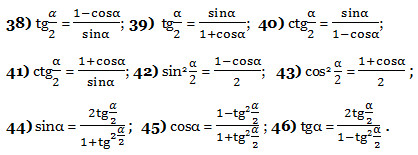
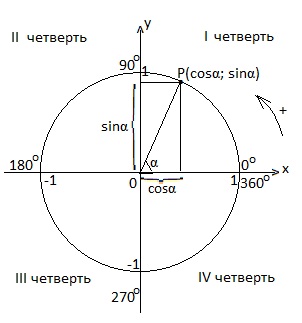
Синус и косинус любого угла

Четность (нечетность) тригонометрических функций

Из тригонометрических функций четная только одна: y=cosx, остальные три – нечетные, т. е. cos (-α)=cosα;

sin (-α)=-sinα; tg (-α)=-tgα; ctg (-α)=-ctgα.

Знаки тригонометрических функций по координатным четвертям

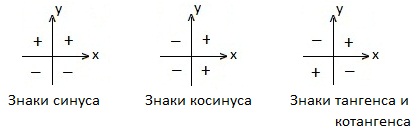
Значения тригонометрических функций некоторых углов

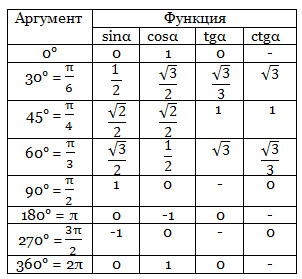
Радианы

1) 1 радиан – величина центрального угла, опирающегося на дугу, длина которой равна радиусу данной окружности. 1 рад.≈57°.

2) Перевод градусной меры угла в радианную.

3) Перевод радианной меры угла в градусную.

Формулы приведения

Мнемоническое правило:

1. Перед приведенной функцией ставят знак приводимой.

2. Если в записи аргумента π/2 (90°) взято нечетное число раз, то функцию меняют на кофункцию.

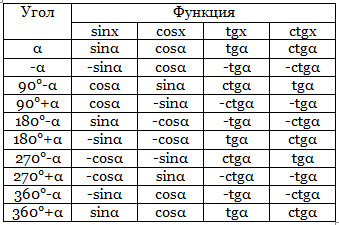
Обратные тригонометрические функции

Арксинусом числа а (arcsin a) называется угол из промежутка [-π/2; π/2 ], синус которого равен а.

arcsin(- a)=- arcsin a.

Арккосинусом числа а (arccos a) называется угол из промежутка [0; π], косинус которого равен а.

arccos (-a)=π – arccosa.

Арктангенсом числа а (arctg a) называется угол из промежутка (-π/2; π/2 ), тангенс которого равен а.

arctg(- a)=- arctg a.

Арккотангенсом числа а (arcctg a) называется угол из промежутка (0; π), котангенс которого равен а.

arcctg (-a)=π – arcctg a.

Решение простейших тригонометрических уравнений

Общие формулы.

1) sin t=a, 0 < a < 1, тогда t=(-1)ⁿ ·arcsin a + πn, nϵZ;

2) sin t = — a, 0 < a < 1, тогда t=(-1)ⁿ⁺¹·arcsin a +πn, nϵZ;

3) cos t=a, 0 < a < 1, тогда t=±arccos a +2πn, nϵZ;

4) cos t =-a, 0 < a < 1, тогда t=±(π-arccos a)+2πn, nϵZ;

5) tg t =a, a > 0, тогда t=arctg a + πn, nϵZ;

6) tg t =-a, a > 0, тогда t= — arctg a + πn, nϵZ;

7) ctg t=a, a > 0, тогда t=arcctg a + πn, nϵZ;

8 ) ctg t= -a, a > 0, тогда t=π – arcctg a + πn, nϵZ.

Частные формулы.

1) sin t =0, тогда t=πn, nϵZ;

2) sin t=1, тогда t= π/2 +2πn, nϵZ;

3) sin t= -1, тогда t= — π/2 +2πn, nϵZ;

4) cos t=0, тогда t= π/2+ πn, nϵZ;

5) cos t=1, тогда t=2πn, nϵZ;

6) cos t=1, тогда t=π +2πn, nϵZ;

7) tg t =0, тогда t = πn, nϵZ;

8 ) ctg t=0, тогда t = π/2+πn, nϵZ.

Решение простейших тригонометрических неравенств

1) sint < a (|a| < 1), -π-arcsina+2πn < t < arcsina+2πn, nєZ.

2) sint > a (|a| < 1), arcsina+2πn < t < π-arcsina+2πn, nєZ.

3) cost < a (|a| < 1), arccosa+2πn < t < 2π-arccosa+2πn, nєZ.

4) cost > a (|a| < 1), -arccosa+2πn < t < arccosa+2πn, nєZ.

5) tgt < a, -π/2+πn < t < arctga+πn, nєZ.

6) tgt > a, arctga+πn < t < π/2+πn, nєZ.

7) ctgt < a, arcctga+πn < t < π+πn, nєZ.

8 ) ctgt > a, πn < t < arcctga+πn, nєZ.

Прямая на плоскости

Общее уравнение прямой: Ax+By+C=0.
Уравнение прямой с угловым коэффициентом: y=kx+b (k – угловой коэффициент).
Острый угол между прямыми y=k₁x+b₁ и y=k₂x+b₂ определяется по формуле:

k₁=k₂ — условие параллельности прямых y=k₁x+b₁ и y=k₂x+b_2.
Условие перпендикулярности этих же прямых:

Уравнение прямой, имеющей угловой коэффициент k, и проходящей

через точку М(х₁; у₁), имеет вид: у-у₁=k (х-х₁).

Уравнение прямой, проходящей через две данные точки (х_1;у₁) и (х₂; у₂) имеет вид:

Длина отрезка М₁М₂ с концами в точках М₁(х_1;у₁) и М₂(х₂; у₂):

Координаты точки М(х_о; у_о) – середины отрезка М₁М₂

Координаты точки С(х; у), делящей в заданном отношении λ отрезок М₁М₂ между точками М₁(х_1;у₁) и М₂(х₂; у₂):

Расстояние от точки М(х_о; у_о) до прямой ax+by+c=0:

Уравнение окружности

Окружность с центром в начале координат: x²+y²=r², r – радиус окружности.
Окружность с центром в точке (a; b) и радиусом r: (x-a)²+(y-b)²=r².

Пределы

Постоянная величина а называется пределом переменной величины х, если эта переменная х при своем изменении неограниченно приближается к а.
Предел постоянной величины равен самой постоянной величине.
Постоянный множитель можно вынести за знак предела.
lim (u±v)=lim u±lim v;
lim (uv)=lim u∙lim v;

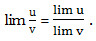
Преобразование (конструирование) графиков функций

График функции y=- f(x) получается из графика функции y=f (x) зеркальным отражением от оси абсцисс.
График функции y=|f(x)| получается зеркальным отражением от оси абсцисс той части графика функции y=f (x), которая лежит ниже оси абсцисс.
График функции y=f(|x|) получается из графика функции y=f (x) следующим образом: оставляют часть графика справа от оси ординат и отображают эту же часть симметрично ей самой относительно оси ординат.
График функции y=A∙f(x) получается из графика функции y=f (x) растяжением в А раз вдоль оси ординат. (Ордината каждой точки графика функции y=f (x) умножается на число А).
График функции y=f(k∙x) получается из графика функции y=f (x) сжатием в k раз при k > 1 или растяжением в k раз при 0 < k < 1 вдоль оси абсцисс.
График функции y=f(x- m) получается из графика функции y=f (x) параллельным переносом на m единичных отрезков вдоль оси абсцисс.
График функции y=f(x)+n получается из графика функции y=f (x) параллельным переносом на n единичных отрезков вдоль оси ординат.

Периодическая функция

Функцию f называют периодической функцией с периодом Т≠0, если для любого х из области определения значения этой функции в точках x, T- x и T+x равны, т. е. выполняется равенство: f(x)=f(T- x)=f(T+x)
Если функция f периодическая и имеет период Т, то функция y=A·f(k∙x+b), где A, k и b постоянны, а k≠0, также периодична, причем, ее период равен T/|k|.

Определение производной.

Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:

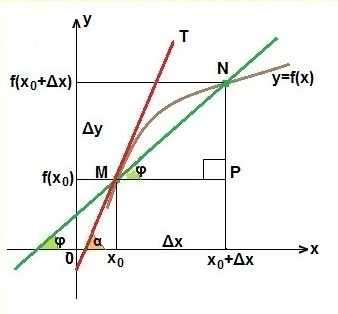
Геометрический смысл производной

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Таблица производных. Примеры вычисления производных

Уравнение касательной к графику функции y=f (x) в точке с абсциссой x₀ имеет вид:

y=f (х₀)+f '(х₀)(х - х₀).

Физический смысл производной.

Если функция y=x (t)описывает путь, по которому прямолинейно движется некоторая точка, то скорость движения этой точки v (t)=x'(t), а ее ускорение a (t)=v'(t).

Основные правила дифференцирования.

Пусть С – постоянная, u=u (x), v=v (x) – функции, имеющие производные.

1) C'=0; 192) x'=1; 2) (u±v)'=u'±v';

3) (Cu)'=C∙u'; 4) (uv)'=u'v+uv';

Формулы дифференцирования.

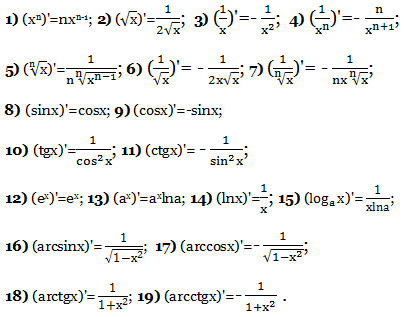
Нахождение функции, обратной данной

1)Выразить переменную х через у;

2)В полученном равенстве вместо х написать у, а вместо у написать х.

Свойства взаимно обратных функций

Графики взаимно обратных функций f (x) и g (x) симметричны относительно прямой у=х

(биссектрисы I и III координатных углов).

Область определения данной функции станет областью значений для обратной функции, а область значений данной функции станет областью определения для обратной функции: D (f)→E (g); E (f)→D (g).

Критическими точками функции называют внутренние точки области определения функции, в которых производная функции равна нулю или не существует.

Возрастание, убывание и экстремумы функции

Функция возрастает на некотором промежутке, если производная данной функции положительна на всем этом промежутке.
Функция убывает на некотором промежутке, если производная данной функции отрицательна на всем этом промежутке.
Если в точке х₀ производная меняет знак с плюса на минус, то точка х₀ является точкой максимума функции.
Если в точке х₀ производная меняет знак с минуса на плюс, то точка х₀ является точкой минимума функции.

Наибольшее и наименьшее значения функции на данном отрезке

Чтобы найти наибольшее и наименьшее значения функции y=f (x) на отрезке [a; b], нужно найти значения этой функции на концах отрезка и в тех критических точках, которые принадлежат данному отрезку, а затем из всех полученных значений выбрать наибольшее и наименьшее.

Схема исследования функции.

1) область определения D (f); 2) четность (нечетность); периодичность; 3) точки пресечения графика с осями координат; 4) промежутки знакопостоянства; 5) промежутки возрастания и убывания; 6) точки экстремума и значения функции в этих точках; 7) поведение функции в окрестности каждой «особой» точки и при больших по модулю значениях х.

Корень n-й степени.

Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.

Свойства корня n-й степени.

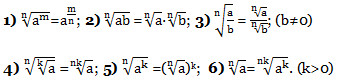
Показательная функция

Функцию вида y=a^x, где а > 0, a≠1, х – любое число, называют показательной функцией.
Область определения показательной функции: D (y)=R - множество всех действительных чисел.
Область значений показательной функции: E (y)=R₊-множество всех положительных чисел.
Показательная функция y=a^x возрастает при a > 1.
Показательная функция y=a^x убывает при 0 < a < 1.

Справедливы все свойства степенной функции:

а⁰=1 Любое число (кроме нуля) в нулевой степени равно единице.
а¹=а Любое число в первой степени равно самому себе.
a^x∙a^y=a^x⁺^y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
a^x:a^y=a^x-^y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(a^x)^y=a^xy При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)^x=a^x∙b^y При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)^x=a^x/b^yПри возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
а^-х=1/a^x
(a/b)^-x=(b/a)^x.

Логарифм числа b по основанию a

Логарифмом числа b по основанию а (log_ab) называют показатель степени, в которую нужно возвести число а, чтобы получить число b.

log_ab=n, если aⁿ=b. Примеры: 1) log₂8=3, т. к. 2³=8;

2) log₅(1/25)=-2, т. к. 5^-2=1/5²=1/25; 3) log₇1=0, т. к. 7⁰=1.

Под знаком логарифма могут быть только положительные числа, причем, основание логарифма — число а≠1. Значением логарифма может быть любое число.

Основное логарифмическое тождество

Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число а, получим число b.

Примеры.

Десятичный логарифм

Логарифм по основанию 10 называют десятичным логарифмом и при написании опускают основание 10 и букву «о» в написании слова «log».

lg7=log₁₀7, lg7 – десятичный логарифм числа 7.

Натуральный логарифм

Логарифм по основанию е (Неперово число е≈2,7) называют натуральным логарифмом.

ln7=log_e7, ln7 – натуральный логарифм числа 7.

Свойства логарифмов справедливы для логарифмов по любому основанию.

Логарифм единицы

log_a1=0 Логарифм единицы равен нулю (a > 0, a≠1).

Логарифм основания

log_aa=1 Логарифм числа а по основанию а равен единице (a > 0, a≠1).

Логарифм произведения

log_a(x∙y)=log_ax+log_ay

Логарифм произведения равен сумме логарифмов сомножителей.

Логарифм частного

log_a(x/y)=log_ax— log_ay

Логарифм частного равен разности логарифмов делимого и делителя.

Основание логарифма и число под знаком логарифма можно поменять местами по формуле:

log_ab=1/log_ba Логарифм числа b по основанию а равен единице, деленной на логарифм числа а по основанию b.

Общая формула перехода к логарифму по другому основанию

log_ab=log_cb/log_ca

Логарифм числа b по основанию а равен логарифму числа b по новому основанию с, деленному на логарифм старого основания а по новому основанию с.

Логарифм степени

log_ab^k=k∙log_ab Логарифм степени (b^k) равен произведению показателя степени (k) на логарифм основания (b) этой степени.

Функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка F'(x)=f (x).
Любая первообразная для функции f (x) на заданном промежутке может быть записана в виде F (x)+C, где F (x)– одна из первообразных для функции f (x), а С – произвольная постоянная.
Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом и обозначается ∫f (x) dx, где f (x) – подынтегральная функция, f (x) dx — подынтегральное выражение, х – переменная интегрирования.

Основные свойства неопределенного интеграла

1) (∫f (x) dx)'=f (x); 2) d∫f (x) dx=f (x) dx; 3) ∫kf (x) dx=k·∫f (x) dx;

4) ∫dF (x) dx=F (x)+C или ∫F'(x) dx=F (x)+C;

5) ∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx;

6) ∫f (kx+b) dx=(1/k)·F (kx+b)+C.

Таблица интегралов.

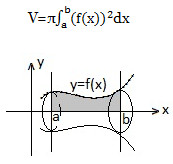
Площадь криволинейной трапеции

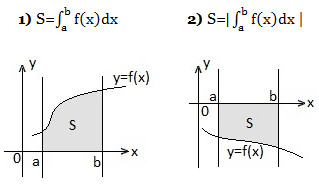
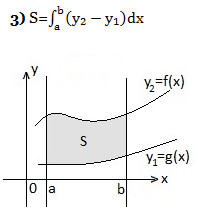
Объем тела вращения.

Алгебра