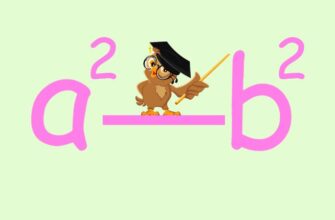7 класс. Алгебра
Больше или меньше? А если "меньше или равно"? Как решить неравенство? В этом уроке мы решим неравенство
Вычислите. 1) 2) 3) 4) Вычисление: 1) В первом примере обратим внимание что мы можем сократить повторяющиеся
Не всегда получается точно измерить длину отрезка или сторону треугольника или длину комнаты.
Чтобы быстро умножить одно число на другое, придумали способ умножения, который упрощает этот процесс.
Как быстро умножать алгебраические выражения? Для этого есть формулы сокращенного умножения, среди них
Если функция задана формулой , где и — некоторые числа, называется линейной функцией. Линейная функция
Очень часто в математике встречаются такие слова «тождество», «тождественно равные», «тождественное преобразование».
7 класс. Алгебра.
I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные
7 класс. Алгебра.
I. Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами
7 класс. Алгебра.
I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются